نصوص للتعجيم مختارة من كل مادة:
![]()
نصوص للتعجيم مختارة من كل مادة:
![]()
النص 1:
تسمى ظاهرة انتشار الماء
عبر الغشاء بالأسموز. وتخضع هذه الظاهرة للقوانين العامة للتنافذ، حيث الحركات
الدائمة والعشوائية للجزيئات المائية تضمن تنافذ هذه الجزيئات وتجانس الوسط
وبالتالي تساوي التوتر بين الوسطين. وتتأثر هذه الحركات بدرجة حرارة الوسط وضغطه.
ويتدفق الماء عبر الغشاء من الوسط الناقص التوتر إلى الوسط المفرط التوتر إلى أن
يحصل تساوي التوتر بين هذين الوسطبن. وتدفق الماء ناتج عن الفرق في ضغط التنافذ
للمحلولين. ويرتبط أساسا ضغط التنافذ لمحلول ما بتركيزه المولي، أي عدد مولات
الجزيئات أو الأيونات المذابة في اللتر الواحد من المحلول.
إن الإنتشار الذي يتم عبر الغشاء يسمى كذلك بالميز الغشائي.
النص 2: آليات التبادلات على مستوى الغشاء السيتوبلازمي
1-
الإنتشار الحر: يتم حسب درجة التركيز، حيث تعبر بعض الجزيئات الغشاء السيتوبلازمي
مخترقة الطبق الدهنية، في حين تكون بعض البروتينات قنوات مائية تسمى القنوات
البروتينية والتي تسمح بمرور الجزيئات من خلالها.
2- الانتشار المسهل: ترتبط البروتينات الناقلة ببعض الجزيئات وتعبر بها الغشاء طبقا
لدرجة التركيز.
3- النقل النشط: تعمل بعض البروتينات الناقلة كمضخات تحمل الجزيئات المنقولة في
اتجاه معاكس لدرجة التركيز. وهذا النوع من النقل يتطلب استهلاك الطاقة الاستقلابية
للخلايا.
النص 3: التبادلات الغازية اليخضورية
النباتات اليخضورية كائنات حية ذاتية التغذية لأنها تحتاج إلى مواد معدنية لتركيب المادة العضوية باستعمال الطاقة الضوئية. وأثناء عملية التركيب هذه، تتم تبادلات غازية بين انبات اليخضوري ووسط عيشه الذي قد يكون مائيا أو هوائيا. وهناك عدة عوامل تؤثر على التبادلات الغازية اليخضورية. فهناك درجة الحرارة، وشدة الإضاءة، وتركيز ثاني أوكسيد الكاربون، وحالة الثغور. ولتحديد مدى تأثير عامل ما، يمكن قياس تغيرات أحجام الغازات المتبادلة حسب تغير العامل المدروس.
النص 4: تركيب النشا
إن تركيب النشا لا يتم إلا إذا توفرت الشروط اللازمة ومنها وجود اليخضور وتوفر كل من الضوء وثاني أوكسيد الكاربون. وهذه الشروط هي نفس الشروط اللازم توفرها لإنجاز التبادلات الغازية اليخضورية. فتركيب النشا والتبادلات الغازية اليخضورية مظهران لنفس الظاهرة التي بموجبها يمتص النبات اليخضوري CO2 وينتج النشا ويطرح O2 بوجود الضوء واليخضور. وتسمى هذه الظاهرة بالتركيب الضوئي.
النص 5: البروتينات
عندما يبلغ عدد الأحماض الأمينية المتحدة 100 أو أكثر في جزيئة واحدة، يصبح عديد البيبتيدات بروتينا. والفرق الأساسي بين عديدات البيبتيدات والبروتينات يكمن في قيمة الكتلة الجزيئية التي تتراوح بين 10000 وبضعة الملايين، بالنسبة للبروتينات التي تعتمد بنيتها الأساسية على الترتيب الخطي للأحماض الأمينية. وكثيرا ما تتغضن أو تلتوي السلسلة على نفسها مكونة بنية جزيئية كروية الشكل وغالبا ما يحصل فيها التغضن والإلتواء معا.
النص 6: بنية البلاستيدة الخضراء
تظهر داخل كل بلاستيدة خضراء ملاحظة بواسطة المجهر الإلكتروني صفيحات ممتدة تتخلل مادة عديمة اللون تسمى الستروما. وتتجمع هذه الصفيحات في مناطق متعددة على شكل أقراص متراكبة مشكلة بذلك ما يسمى بالكرانومات.
النص 7: التقاط الطاقة الضوئية
إن التنظيم الملاحظ بين جزيءات غشاء التيلاكويد وجزيئات الصبغات اليخضورية يمكن من تجميع الطاقة الملتقطة من طرف كل الصبغات المتواجدة (اللاقطة المجمعة)، وتوجيهها إلى جزيئة واحدة من اليخضور a التي تصبح في حالة اهتياج، إذ تصبح بعد توصلها بالطاقة قابلة لتحرير إلكترون واحد. وتسمى هذه الوحدة الوظيفية التي تتضمن كلا من اللاقطة المجمعة وجزيئة اليخضور a نظاما ضوئيا.
النص 8: الخاصيات العامة للتنفس والتخمر
يمكن إبراز هذه الخاصيات انطلاقا
من دراسة حالة خميرة البيرة. خميرة البيرة، فطر مجهري وحيد الخلية مسؤول عن التخمر
الكحولي. تستعمل هذه الخميرة الكليكوز كمستقلب طاقي ويمكنها هدمه بطريقتين مختلفتين
حسب ضروف الزرع:
- إذا كان الوسط غنيا بالأكسجين (وسط حيهوائي) وتركيز الكليكوز فيه ضعيفا، يتم
الهدم الكلي لجزيئة الكليكوز وتحويلها إلى ثاني أوكسيد الكربون والماء، وهذا يدل
على أن الخمائر تتنفس.
- عكس ذلك إذا كان الوسط مفتقرا إلى الأكسجين (حي لاهوائي) أو إذا كان تركيز
الكليكوز مرتفعا جدا في هذا الوسط، يتم هدم الكليكوز إلى إيثانول وثاني أوكسيد
الكربون، ويتعلق الأمر في هذه الحالة بالتخمر.
النص 9: انحلال الكليكوز
إنحلال الكليكوز عبارة عن مجموعة
من تفاعلات كيميائية تتم على مستوى الجبلة الشفافة وتنشطها أنزيمات نوعية. خلال هذه
الظاهرة تتحول كل جزيئة من الكليكوز فوسفاط (C6P)
إلى جزيئتين من حمض البيروفيك. يمكن تقسيم انحلال الكليكوز إلى ثلاث مراحل:
- في المرحلة الأولى يتحول الكليكوز فوسفاط إلى فروكتوز ثنائي الفوسفاط (C6
diP) بعد تثبيت مجموعة فوسفاتية آتية من ATP.
- في المرحلة الثانية ينشطر الفروكتوز ثنائي الفوسفاط إلى جزيئتين من سكر ثلاثي
فوسفاط (2C3-P). تخضع كل من هاتين الجزيئتين إلى
انتزاع الهيدروجين (أي أكسدة). ]ثبت الهيدروجين على جزيئة ناقلة للهيدروجين:
(Nicotinamide - Adénine - Dinucléotide) أو NAD+.
التي تتحول من شكلها المؤكسد (NAD+)إلى
شكلها المختزل (NADH2). يكون هذا التفاعل أكسدة
-اختزال مقرونا بتفسفر جزيئتي C3 P التان
تتحولان إلى جزيئتين من P-C3 P.
- في المرحلة الثالثة تسلم جزيئتا P-C3 P
مجموعتيهما الفوسفاتية إلى ADP وتتحولان إلى جزيئتين من حمض
البيروفيك بينما تتحول جزيئات ADP إلى ATP.
النص 10: التقلص العضلي
يهدف التقلص العضلي إلى إنتاج قوة عضلية، فإذا كان طرفا العضلة غير مثبتين، فإن التقلص يقربهما من بعضهما، أما إذا كان أحد الطرفين فقط غير مثبت فإن التقلص يقرب النهاية المتحركة من النهاية المثبتة وهذا ما يحدث في غالب الأحيان خلال العمل الطبيعي للعضلة. أما إذا كانت النهايتان ثابتتين، فإن التقلص لا ينتج أي تقصير في طول العضلة ولكنه يجعل العضلة في حالة توتر، إذن هناك نوعان من التقلصات العضلية: أحداهما متساوي التوتر، والآخر متساوي القياس.
النص 11: دراسة التقلص العضلي
التقلص العضلي هو الإستجابة
الطبيعية لعضلة للإهاجة، نقول إن العضلة قلوصة وتسمى هذه الميزة بالقلوصية.
عند تسليط إهاجة واحدة على العضلة يكون التقلص مختصرا جدا ومنفردا، يتعلق الأمر
برعشة عضلية معزولة، يمكن تقسيمها إلى ثلاث مراحل:
1- زمن الكمون أو الزمن الضائع هو الفترة الزمنية الفاصلة بين لحظة الإهاجة وبدابة
الإستجابة.
2- مرحلة التقلص خلالها يرتفع التوتر أو القوة المبذولة، في حالة تقلص متساوي
القياس، أو ينقص الطول تدريجيا في حالة تقلص متساوي التوتر.
3- مرحلة الإرتخاء: خلاله تسترجع العضلة أبعادها الأولية وتكون مدة هذه المرحلة
أطول شيئا ما من مدة مرحلة التقلص.
النص 12: ملاحظة ليف عضلي بالمجهر الإلكتروني
تبين ملاحظة مقاطع طولية لليف عضلي بالمجهر الإلكتروني نمطا ثانيا من البنيات الطولية: الخييطات العضلية. وهناك صنفين من الخييطات: خييطات سميكة، مكونة من بروتين يسمى الميوزين، وخييطات دقبقة مكونة من بروتين آخر يسمى الأكتين، يرتبط بهذا الأخير بروتينان آخران: التروبونين والتروبوميوزين.
النص 13: وظائف البروتيدات
تختلف وظائف البروتيدات حيث يمكن
التمييز بين:
- بروتيدات البنية: وتشكل المكونات الأساسية لخلايا المتعضيات، إذ أنها
تكون هيكل الخلايا الذي يمنحها شكلها الخاص (بروتيدات الغشاء السيتوبلازمي،
الكولاجين، الأنيببات الدقيقة السيتوبلازمية ...).
- الأنزيمات: ويمكن هذا الصنف من البروتيدات من تحفيز أغلبية التفاعلات
الكيميائية الخاصة بالتحلل والبناء.
- الأجسام المضادة: يركب الجسم هذه البروتيدات كرد فعل ضد دخول العناصر
الأجنبية للجسم.
- الحاثات: جزيئات بروتيدية حاملة للمعلومات، تنقل بواسطة الدم من مكان
تركيبها (الغدد) إلى الخلايا حيث تمارس تأثيرها الفيزيولوجي.
النص 14: تحديد موقع تركيب البروتيدات والمسير الضمخلوي للجزيئات البروتيدية المركبة
يبين المسار الضمخلوي للبروتيدات، الإستمرارية الموجودة بين مختلف الأجزاء السيتوبلازمية المحاطة بغشاء: الشبكة السيتوبلازمية، جهاز غولجي، الكييسات ةالحويصلات الغولجية، حويصلات الإفراز، علاوة على الغشاء السيتوبلازمي، حيث يجب التأكيد على وجود هذة الإستمرارية في الزمان والمكان، إذ يضمن التدفق الغشائي التحول والإنتقال التدريجي من جزء خلوي لآخر. وبالتالي يبدو هذه العناصر كمناطق مفروقة ومختصة لنظام غشائي يتجدد باستمرار.
النص 15: الإنعكاس الفطري
يستلزم كل انعكاس فطري العناصر
الأساسية التالية:
1. مستقبلات حسية تستقبل المهيج وتنشأ على مستواها سيالات عصبية.
2. موصل حسي يتكون من ألياف عصبية حسية (ألياف موردة) تنقل السيالاات
العصبية المركزية.
3. مركز عصبي انعكاسي يستقبل السيالات العصبية الحسية وتنشأ على مستواه
سيالات عصبية حركية.
4. موصل حركي يتكون من ألياف عصبية حركية (ألياف مصدرة) تنقل السيالات
العصبية النابذة.
5. مستجيب.
النص 16: أصل جهد العمل
على إثر تهييج الليف العصبي
ينعكس الإستقطاب الغشائي على مستوى المنطقة المهيجة، فيترتب عنه تغيير في توزيع
الأيونات من جهتي الغشاء الخلوي. وتتم التغيرات المصاحبة لجهد العمل على ثلاث
مراحل:
أ- ترتفع نفاذية غشاء الليف العصبي لأيونات
Na+ بكيفية سريعة ومهمة
يترتب عنها دخول متفجر لأيونات Na+
ويحدث هذا الدخول إزالة استقطاب الغشاء.
ب- ترتفع النفاذية الغشائية لأيونات K+
بوتيرة ضعيفة وبطيئة بالمقارنة مع أيونات Na+
ينتج عنها خروج تدريجي وبطيء نسبيا لإيونات K+
. ويؤدي هذا الخروج إلى إعادة استقطاب الغشاء. أما استمرار خروج
K+ فينتج عنه استقطاب زائد أو مفرط.
ج- بفضل المضخات الأيونية يتم الرجوع إلى التركيزات الأصلية لأيونات
Na+ و
k+ كما كانت عليه أثناء جهد الكمون.
النص 17: بنية العصب
يتكون العصب من حزم من الألياف العصبية تحاط كل واحدة منها بنسيج ضام سميك، ويفصل بين مختلف الحزم نسيج ضام مرتخ يحتوي على عروق دموية. تظهر الملاحظة بتكبير قوي لجزء من المقطع العرظي لهذا العصب أليافا عصبية مستديرة وذات قطر متفاوت. يتكون كل ليف عصبي من عنصر مركزي يدعى المحورة، يحيط بها غمد من النغاعيين.
النص 18: بنية السينابس
تتفرع محورة العصبة عند نهايتها
مشكلة التشجر النهائي. وينتهي كل فرع من هذا التشجر بحبة سينابسية تعتبر بمثابة
رابط بين عصبتين مختلفتين: العصبة قبل السينابسية والعصبة بعد السينابسية.
تمكن الملاحظة بالمجهر الإلكتروني التمييز بين نمطين من السينابسات: سينابس ذات
تبليغ كيميائي وسينابس ذات تبليغ كهربائي.
النص 19: أهم المبلغات العصبية
بينت التحاليل الكيميائية أن
المادة المبهمة هي الأستيلكولين، والمادة الودية هي النورادرينالين. ولقد سمحت
تقنيات حديثة باكتشاف مبلغات عصبية أخرى (دوبامين، سيروطونين، ...
يستلزم تركيب المبلغات العصبية بشائر (الكولين، الأحماض الأمينية، ...)
وأنزيمات. كما يتطلب هذا التركيب طاقة على ATP وبنيات مختصة
(جهاز غولجي، أجسام Nissl ...).
النص 20: التواصلات الهرمونية
بالتوازي مع التواصل العصبي الذي
تتبادل الخلايا أثناءه وعن بعد رسائلة مستعملة في ذلك شبكة من العصبات والإتصالات
السينابسية، هناك التواصل الهرموني الذي يعتمد على تبادل رسائل تنتشر في الوسط
الداخلي المحيط بالخلايا. وهذه الرسائل الكيميائية أي الهرمونات أو الإفرازات
العصبية هي مواد:
- تنتجها خلايا غدية صماء أو عصبية غدية.
- تحرر في الدم الذي يؤمن توزيعها على الخلايا الهدف.
- تحدد على مستوى هذه الأخيرة إجابة فيزيولوجية متكيفة.
النص 21: بنية البنكرياس
البنكرياس غدة لها شكل ورقة
خضراء ممتدة، تقع خلف المعدة وتتكون من مجموعتين من الخلايا: بارانشيم غدي (عنبات)
تتدخل في الهضم وجزيرات لنجرهانس التي تتدخل في استقلاب الكليكوز.
إن الخلايا المسؤولة عن الإفرازات الهرمونية والمتجمعة في جزيرات لنجيرهانس هي
من صنفين: الخلايا α والخلايا β. وقد
تمكن الباحثون من الكشف عنها بواسطة تقنية التلوين المسماة بالتحصين التفلوري حيث
تم استعمال مضادات الأجسام تلتصق بطريقة اختيارية إما بالأنسلين أو بالكليكاكون.
وتحمل مضادات الأجسام جزيئات متفلورة تسمح بتمييز الخلايا المفرزة للأنسلسن عن
الخلايا المفرزة للكليكاكون.
النص 22: تنظيم تحلون الدم
إن تنظيم
تحلون الدم يخضع لصنفين من الأخبار المتعارضة، أحدهما مخفض لنسبة السكر في الدم (الأنسلين)
والآخر باعث للسكر في الدم (الكليكاكون). وثبات تحلون الدم مرتبط بتوازن هاذين
الخبرين. ولكن هذا التوازن ليس مستقرا حيث يتم تعديله في كل لحظة. فالخلايا
الهرمونية يجب أن تتوفر في كل لحظة على معلومات تتعلق بنسبة الكليكوز في الدم حتى
تتمكن من تصحيحها بسرعة. ويتم إخبار الخلايا الهرمونية بواسطة الكليكوز. وقد بينت
الدراسة التجريبية أن تحرير الأنسلين يرتفع سريعا عندما يرتفع تركيز الكليكوز
الدموي، بينما ارتفاع تحلون الدم يمنع ارتفاع الكليكاكون. وأما انخفاض تحلون الدم
فيرفع إفراز الكليكاكون. إذن فنسبة الكليكوز الدموي هي التي تحدث تحرير الأنسلين أو
الكليكاكون من قبل خلايا جزيرات لنجرهانس.
وهكذا فتحلون الدم ينظم بنسبة الكليكوز الدموي. يتعلق الأمر إذن بتنظيم ذاتي،
بحيث إذا ارتفع تحلون الدم يزداد إفراز الأنسلين وينقص إفراز الكليكاكون، مما يؤدي
إلى انخفاض تحلون الدم وعودته إلى القيم العادية.
النص 23: تنظيم الضغط الشرياني
يؤمن الجهاز الدوراني توزيع عدة مواد في الجسم كالقيت والأوكسيجين والهرمونات. ويتكلف بصرف الفضلات كثاني أكسيد الكربون، والحمض البولي ... ويتمكن الجهاز الدوراني من القيام بهاتين الوظيفتين الأساسيتين بفضل دوران الدم تحت ضغط معين. ينطلق الدم دوريا من القلب ليعود إليه بعد الدوران في الشرايين والشعيرات والأوردة. وتتكرر هذه الدورة بدون توقف وفي نفي الإتجاه. يعتبر القلب إذا العضو المحرك للدورة الدموية.
النص 24: تنظيم الضغط الشرياني
يتم
تنظيم الضغط الشرياني بواسطة ميكانيزمات عصبية لاإرادية تتدخل فيها العناصر
التالية:
- مستقبلات حسية: مستقبلات الضغط، وهي متمركزة في مستوى قوس الأبهر والجيب
السباتي، وتستجيب لكل ارتفاع في الضغط الشرياني.
- مسالك موردة وتتمثل في الألياف العصبية المتصلة بمركز البصلة السيسائية
القلبي، وتنقل السيالة العصبية الناتجة عن نشاط مستقبلات الضغط نحو المركز المبطئ
للقلب.
- مسالك مصدرة وهي من نوعين:
. الألياف اللاودية التس تبطئ القلب وبالتالي تخفض الضغط الشرياني
(ألياف عصب X).
. الألياف الودية التي تسرع القلب وتضيق الأوعية الدموية وبالتالي ترفع
من قيمة الضغط الشرياني.
![]()
النص 01:
ننجز تجربة السقوط الحر في الهواء
مستعملين جسما انسيابي الشكل وذا كثافة عالية (كرية فولاذية). ونختار ارتفاعات
السقوط غير كبيرة جدا بحيث يمكن، في هذه الظروف إهمال تأثير الهواء بالنسبة لتأثير
الأرض.
يبكي الكهرمغناطيس الكرية في الموضع الأعلى وعند فتح
قاطع التيار، تتحرر الكرية فتسقط بدون سرعة بدئية أمام مسطرة رأسية مدرجة. تمكن
خلية كهرضوئية، مرتبطة بميقت إلكتروني من تعيين المدة
Δt التي يستغرقها مرور الكرية أمام الخلية.
النص 02: تمرين
تتغير سرعة جسم صلب في
إزاحة بدلالة الزمن. إثناء حركة الحسم، تبقى إحدى القوى المطبقة على الجسم ثابتة،
شدتها F=200N، ومنحاها معاكسا لمنحى الحركة.
1. مثل
مبيانيا تغيرات قدرة هذه القوة بدلالة الزمن.
2. عين مبيانيا شغل هذه القوة بين
اللحظتين t=0، و t=9s.
النص 03:
ليكن (S) جسا صلبا في حركة دوران حول محور ثابت
(Δ) يمر بالنقطتين A و B. أثناء الدوران جميع نقط الجسم S تتحرك وفق
دائرة ماعدا النقط المنتمية إلى المحور Δ التي تبقى في حالة
سكون: بالنسبة للنقطتين M و N مثلا،
نلاحظ أنهما ترسمان بالتتابع مسارين دائريين ممركزين على المحور Δ عند النقطتين
O و Ơ، مستوى كل منهما عمودي على Δ، أما بالنسبة للنقطتين
A و B فإنهما لا تتحركان عندما يدور
S.
النص 04: معلمة نقطة من الحسم الصلب
لدراسة حركة النقطة M من الجسم الصلب S، نختار معلما متعامدا
ممنظما بحيث تكون المتجهة الواحدية
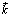 منطبقة مع محور الدوران
ويكون المستوى
منطبقة مع محور الدوران
ويكون المستوى 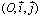 منطبقا مع مستوى مسار حركة هذه النقطة،
كما نعتبر المحور x'x الذي يحمل المتجهة
منطبقا مع مستوى مسار حركة هذه النقطة،
كما نعتبر المحور x'x الذي يحمل المتجهة
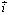 اتجاها مرجعية.
اتجاها مرجعية.
وهكذا يمكن تعيين موضع
النقطة M في كل لحظة:
- بمعرفة أفصوله
المنحني s على مسار النقطة M.
- أو بمعرفة أفصوله الزاوي
θ .
تربط الأفصول المنحني والأفصول الزاوي العلاقة :
s=R.θ
النص 05: تطبيق
نعتبر
بكرة P ذات مجريين شعاعاهما على التوالي
R1=20cm و
R2=10cm،
تدور بسرعة زاوية ω ثابتة حول نفس المحور الأفقي Δ في المنحى المبين في الشكل
جانبه.
الخيطان f1 و f2 الملفوفان على مجريي البكرتين يحملان في طرفيهما
الحرين جسمين
S1 و S2 . نفترض أن الخيطين غير قابلين للإمتداد ولا ينزلقان
على المجريين.
- احسب سرعة كل من
S1 و S2
عندما يكون تردد الدوران
N=10tr/s.
النص 06: تعريف عام للمزدوجة
المزدوجة مجموعة قوى مستوائية، بحيث:
- مجموع متجهات هذه القوى مجموع
منعدم.
- يميزها عزم ثابت، بالنسبة لأي محور متعامد مع المستوى الذي توجد
فيه.
إن هذا التعريف يشمل ويتجاوز المعنى المنحصر لكلمة
مزدوجة بمدلولها على شيئين اثنين (قوتان ...) ونستعمله في الفيزياء كلما كان العزم
كافيا لتمييز تأثير ما دون الحاجة إلى القوى التي تمثل هذا التأثير. ففي هذا الإطار
نذكر: مزدوجة محركة، مزدوجة مقاومة، مزدوجة الكبح ...
النص 07: تمرين
نعتبر
عارضة OA متجانسة، أسطوانية الشكل، قطرها d=1,2m وطولها l=1,2m وكتلتها m=1kg. يمكن للعارضة أن تدور بدون احتكاك حول محور ثابت Δ أفقي يمر
بطرفها O. نضع في النقطة C التي تنتمي
إلى الخط الرأسي المار من الطرف O، خلية كهرضوئية متصلة بميقت
إلكتروني يمكن بواسطتها قياس المدة Δt لمرور الطرف A أمام
الخلية لأول مرة.
نطلق العارضة من الموضع الأفقي، المبين على
الشكل، بدون سرعة بدئية فنجد Δt=0,002s.
1. احسب شغل كل
من القوى المسلطة على العارضة بين لحظة انطلاقها ولحظة مرورها لأول مرة من الخط
الرأسي.
2. أوجد سرعة مركز قصور العارضة لحظة مرورها لأول مرة من الخط
الرأسي.
3. استنتج الطاقة الحركية للعارضة لحظة مرورها لأول مرة من الخط
الرأسي.
النص 08: تعبير طاقة الوضع الثقالية
ليكن حسم صلب S، كتلته m، في سقوط حر في مجال الثقالة g الذي نعتبره منتظما. نمعلم مواضع مركز القصور G للجسم S في معلم ممنظم
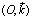 محوره z'z رأسي ومتجه نحو
الأعلى.
محوره z'z رأسي ومتجه نحو
الأعلى.
نعبر عن شغل وزن الجسم S أثناء
انتقاله بين الموضعين G1 و G2، أنسوباهما بالتتابع z1 و z2 ،
بالعلاقة: W(P)=P.G1G2
نلاحظ أن
شغل وزن الجسم S يظهر كفرق لحدين:
- mgz1 الذي يمثل طاقة تتعلق بالأنسوب z1 وتوافق طاقة الوضع للجسم S عند
هذا الأنسوب.
- mgz2 الذي يمثل طاقة تتعلق
بالأنسوب z2 وتوافق طاقة الوضع للحسم S عند هذا الأنسوب.
النص 09: النواس الوازن
النواس الوازن هو كل جسم صلب يمكنه الدوران حول
محور Δ أفقي ثابت لا يمر بمركز قصوره G.
يأخذ النواس الوازن موضعين للتوازن
يتعلقان بالتوازن المستقر والتوازن غير المستقر . نزيح النواس الوازن عن موضع
توازنه المستقر، ثم نحرره بدون سرعة بدئية. نفترض أن الإحتكاك
مهملا.
نلاحظ أن النواس يتأرجح حول موضع توازنه المستقر.
نقول إن النواس ينجز حركة تذبذبية حول هذا الموضع.
يخضع
النواس لوزنه P وللقوة R التي يطبقها
المحور Δ. بتطبيق مبرهنة الطاقة الحركية على النواس عندما ينتقل مركز قصوره G من الموضع G1 أنسوبه z1 إلى الموضع G2
أنسوبه z2 :
ΔEc=WP+WR
لكن WR=0 لكون خط تأثير R يمر بالمحور
Δ في غياب الإحتكاك. إذن ΔEc=Ep1-Ep2.
ملحوظة: في الواقع، ينتهي النواس الوازن بالتوقف عن التذبذب في موضعه المستقر لكونه يفقد تدريجيا الطاقة الميكانيكية، المكتسبة سابقا، بسبب وجود احتكاكات ناتجة عن تأثير الهواء والمحور Δ.
النص 10: طريقة تحليل تمارين تتعلق بالطاقة الميكانيكية
يمكن اتباع الخطوات التالية عند حل
كل تمرين مستعملا الطاقة الميكانيكية:
1.
اختيار الجسم أو المجموعة.
2. اختيار الحالة المرجعية (إن لم تكن مفروضة).
3.
تحديد الحالة البدئية والحالة النهائية.
4. التعبير عن الطاقة الحركية وطاقة
الوضع الثقالية للجسم أو المجموعة في الحالتين البدئية والنهائية.
5. كتابة
معادلة انحفاظ الطاقة الميكانيكية.
النص 11: تعريف ضغط غاز
نعرف
الضغط P لغاز بالعلاقة P=F/S حيث ترمز
F إلى شدة القوة الضاغطة وتدل S على
مساحة سطح الجسم الذي يتم عليه تأثير الغاز. وحدة الضغط في النظام العالمي للوحدات
هي الباسكال ونرمز لها ب Pa .
الباسكال
هو قيمة الضغط الناتج عن التأثير الموزع لقوة ضاغطة شدتها 1N
على مساحة 1m2 أي: 1Pa=1N/m2 .
يجب التمييز بين الضغط والقوة الضاغطة.
فالضغط مقدار سلمي موجب ويمكن تعريفه في كل نقطة من غاز. أما القوة الضاغطة فهي
مقدار متجهي ولا يمكن تسليطها إلا على مساحة أي مجموعة من نقط.
النص 12:
ينتج
عن ارتفاع درجة الحرارة T لغاز ما تزايد الإرتجاج الجزيئي (أي
تزايد السرعة المتوسطة للجزيئات). وبما أن عدد الجزيئات والحجم لا يتغيران فإن
تزايد السرعة المتوسطة يؤدي في آن واحد إلى تزايد عدد تصادمات الجزيئات مع جوانب
الإيناء وحدتها. الشيء الذي يؤدي إلى ارتفاع ضغط الغاز.
النص 13: التبخير والتكاثف
التبخير هو ظاهرة تحول جسم من الحالة السائلة إلى الحالة الغازية. ويمكن أن يحدث
هذا التحول بطرق متنوعة، منها مثلا تبخر سائل عند تركه في الهواء الطلق أو غليانه
بالتسخين.
فالماء يتبخر ولو عند درجات حرارة أصغر من 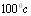 .
.
النص 14:
تتعلق
حرارة التفاعل بكتل المتفاعلات وبالشروط التجريبية (درجة الحرارة، الضغط، الحالة
الفيزيائية للمتفاعلات والنواتج، ...)، ولذا يجب أن يحدد في المعادلة الحصيلة:
- درجة الحرارة والضغط.
- كمية مادة
أحد المتفاعلات أو أحد النواتج.
- الحالة الفيزيائية
لمتفاعلات ونواتج التفاعل.
النص 15: المجال الكهرساكن المحدث من طرف شحنتين
نعتبر على التوالي في نقطتين A و B شحنتين نقطيتين QA و QB كلتاهما مصدر للمجال. نريد تعيين المجال الكهرساكن E المحدث من طرف QA و QB معا في نقطة M . لنعتبر شحنة نقطية q في M. تحدث الشحنة QA في النقطة M مجالا كهرساكنا EA بحيث تطبق QA على q قوة كهرساكنة FA ، وتحدث أيضا الشحنة QB مجالا كهرساكنا EB في نفس النقطة M بحيث تطبق QB على q قوة كهرساكنة FB وتطبق QA و QB في نفس الوقت على q قوة كهرساكن F.
النص 16: قانون جول
عند مرور التيار الكهربائي، اكتسب الموصل الأومي (AB) طاقة كهربائية Er خلال المدة t وأعطى طاقة حرارية Q. وبما أن الموصل الأومي لا يمكنه أن يختزن الطاقة المكتسبة، فسيعطيها للمحيط الخارجي على شكل طاقة حرارية فقط.
النص 17: المولد المؤمثل للتوتر
إن معادلة المميزة (شدة التيار -
التوتر) لمولد كهربائي يشتغل في مجاله الخطي هي: UPN=E-r.I.
فإذا كانت المقاومة
الداخلية منعدمة، تكون UPN=E (كيفما كانت شدة
التيار I أصغر من القيمة القصوية Imax ) ويسمى المولد في هذه الحالة مولدا مؤمثلا
للتوتر.
النص 18: الدراسة التجريبية لمستقبل كهركيميائي (المحلل الكهربائي)
نعتبر المحلل الكهربائي المكون من
الكترودين من البلاتين (أو الكربون) نغمرهما في محلول مائي لحمض الكبريتيك. يكون
هذا المحلل الكهربائي ثنائي قطب (AB).
ويمكننا أن نخط مميزته (شدة التيار - التوتر) بالطرق المعتادة. نلاحظ أن جزء
المنحنى (MN) مستقيم معامله الموجه موجب ولا يمر بأصل
المحورين. ويمكن كتابة معادلة المستقيم الحامل له كما يلي: UAB=E'+r'.I
'E: القوة
الكهرمحركة المضادة للمحلل الكهربائي، وحدتها الفولط (V).
وتمثل بالنسبة لهذا المستقيم الأرتوب عندما تنعدم شدة التيار.
'r:
المقاومة الداخلية للمحلل الكهربائي (بالأوم
Ω). وتمثل المعامل الموجه
للمستقيم.
النص 19: المولدات الكهركيميائية
تضمن
هذه المولدات تحويل الطاقة الكيميائية إلى طاقة كهربائية انطلاقا من التفاعلات
الكيميائية التي تحدث عند إلكتروديها المغمورين في الإلكتروليت حيث يكون
الإلكترودان قطبي المولد.
وتنتمي الأعمدة والمراكم للمولدات
الكهركيميائية. فالأعمدة لا يمكنها أن ترجع إلى حالتها البدئية إذا ما أعطت طاقتها
لمحيطها الخارجي، بعكس المراكم التي يمكن شحنها من جديد بربطها بجهاز يكسبها الطاقة
التي أضاعتها.
النص 20: العمود الضوئي
ثنائي
قطب يحول مباشرة جزءا من الطاقة الشمسية التي يكتسبها إلى طاقة كهربائية.
تصنع الأعمدة الضوئية المتداولة حاليا على شكل لويحات صغيرة
لا تتجاوز مساحتها بعض السنتيميرات المربعة، ويتراوح سمكها ما بين 200μm و 300μm .
ويتكون
العمود الضوئي أساسا من السيليسيوم، وينشط وجهه المعرض للشمس بعنصر آخر كالفوسفور
مثلا، ونحصل على التيار الكهربائي بتعدين الوجه الخلفي للويحة وبتثبيت شبكة على
الوجه الأمامي.
يكافئ العمود الضوئي مولد تيار مستمر قوته
الكهرمحركة 0,5V تقريبا. وللحصول على قدرة أكبر تستجيب
للإستعمالات العملية، يتم تجميع عدد كبير من الأعمدة الضوئية على التوالي لرفع
التوتر وعلى التوازي لرفع شدة التيار. وتستعمل الأعمدة الضوئية كمولد للطاقة
للأقمار الإصطناعية، وفي بعض محطات الترحيل الهرتزية التي توجد في مناطق
معزولة.
النص 21: تمرين
هل يمكن قياس القوة الكهرمحركة لمستقبل ؟
عرف وأعط تعبير مردود مستقبل ومولد.
هل يسخن محرك بكيفية خطيرة عندما تمنعه من الدوران ؟
هل يمكن لمركم أن يكون مستقبلا ؟
هل يمكن لكل المولدات أن تشتغل كمستقبلات ؟
النص 22: تعيين القدرة المبددة في منظم متكامل للتوتر
المنظم المتكامل للتوتر مركبة إلكترونية لها ثلاثة مرابط وتستعمل خاصيات المضخم العملياتي، وتمكن من الحصول على توتر Us مستمر ومثبت عند الخروج بين المربطين عندما نطبق توترا مستمرا أو مستمرا تقريبا. كما أنها تحول الطاقة الكهربائية التي يكتسبها عند مدخله إلى طاقة كهربائية يمكن استعمال جزء منها عند مخرجه.
النص 22: الظواهر الإهتزازية المخمدة
عندما
نزيح الطرف الحر لشفرة، مثبتة على ملزمة، عن موضع توازنها فأنها تنجز حركة اهتزازية
حول هذا الموضع. لكن سرعان ما نلاحظ أن حركتها الإهتزازية تتغير، إذ يتناقص وسع
التذبذبات تدريجيا إلى أن تتوقف. نقول، في هذه الحالة، إن التذبذبات تتخمد وإن حركة
المتذبذب مخمدة.
وتجدر الإشارة أنه خلال التذبذبات تتحول
طاقة الوضع إلى طاقة حركية والعكس صحيح. وبما أن المجموعة غير معزولة، فإن خمود
التذبذبات يعزى غلى تبدد الطاقة الميكانيكية حيث إن نسبة لا بأس بها من هذه الطاقة
تضيع بسبب الاحتكاكات.
النص 23: الدور والتردد
عند صيانة اهتزازات متذبذب، صيانة
ملائمة، فإنها تتكرر بانتظام وبكيفية مماثلة. نقول إن الاهتزازات
دورية.
نسمي دورا المدة الزمنية التي تتكرر فيها الظاهرة
بكيفية مماثلة ونرمز لها بـ: T. ويكمن تمييز الظاهرة كذلك
بترددها N. يساوي تردد ظاهرة اهتزازية عدد أدوار هذه الأخيرة
في ثانية واحدة: N=1/T.
في النظام
العالمي للوحدات، وحدة الدور هي الثانية، ووحدة التردد هي الهرتز. نستعمل كذلك
مضاعفات الهرتز للتعبير عن التردد.
النص 24: معاينة اهتزازة صوتية على شاشة راسم التذبذب
يمكن الحصول على منبع صوتي بتغذية
مكبر الصوت بمولد ذي تردد منخفض (GBF). وتلتقط الإهتزازت
الصوتية المحصل عليها بواسطة ميكروفون موضوع قرب مكبر الصوت.
نربط المولد والميكروفون براسم التذبذب.
نستعمل نفس الحساسية بالنسبة للمدخلين YA و YB . يظهر على الشاشة منحنيين جيبيين لهما نفس الدور.
الأول يمثل الاهتزازات الصوتية الملتقطة من المنبع (المولد) والثاني يمثل نفس
الاهتزازات الملتقطة من الميكروفون. ويمكن أن نستخلص من هذه التجربة :
- أن الاهتزازات
الصوتية دورية ويمكن قياس دورها.
- أن دور
الإهتزازات الصوتية يساوي دور المنبع الصوتي.
النص 25: الإشارات ووسط الانتشار
يمكن اعتبار مختلف الإشارات ( المستعرضة والطويلة و اللي)، إشارات ميكانيكية، حيث إنها تؤثر في الخواص الميكانيكية لوسط الإنتشار، وذلك بتغيير الموضع والسرعة أي تغيير طاقة الوضع والطاقة الحركية للمادة المكونة لوسط الانتشار. وتجدر الإشارة إلى أن خلال انتشار الإشارات الميكانيكية، تنتقل الطاقة وليس المادة. ولكي تنتشر هذه الإشارات، يجب أن يكون وسط الإنتشار مرنا. إن الصوت ينتشر في عدة أوساط مادية ولا ينتشر في الفراغ.
النص 26: الإشارات الكهرمغناطيسية
لكي يصلنا الضوء المنبعث من الشمس
ومن مختلف النجوم، عليه أن يعبر فضاءات شاسعة وفارغة، وبالتالي فإنه ينتشر في
الفراغ، مثل الإشارات الكهرإذاعية عكس الإشارات الميكانيكية التي تستلزم وسطا ماديا
مرنا لكي تنتشر. فإن هناك إشارات لا تستلزم وسطا ماديا لإنتشارها تسمى الإشارات
الكهرمغناطيسية ومن بين المقادير الفيزيائية التي تتغير بسبب انتشار إشارة
كهرمغناطيسية يوجد المجال الكهربائي.
ويمكن للإشارات
الضوئية أن تنتشر في أوساط مادية شفافة لكن بسرعة اقل من سرعة انتشارها في الفراغ
ولا يمكنها أن تنتشر في أوساط معتمة. وتجدر الإشارة إلى أن الإشارات الكهرمغناطيسية
تحمل طاقة تسمى الطاقة الكهرمغناطيسية (الطاقة الشمسية).
النص 27: المظهر الطاقي للموجة المتوالية
عندما يهتز الهزاز، فإنه ينجز شغلا، ويمد الحبل بطاقة ميكانيكية، هذه الأخيرة لا تبقى منحصرة عند المنبع S، بل تنتشر طول الحبل صحبة الموجة، مما يجعل كل نقطة من الحبل تهتز بدورها عند مرور الموجة. يصاحب انتشار الموجة، احتكاكات داخلية، وأخرى خارجية مثل الإحتكاكات بين الحبل والهواء والحبل والحامل. ولهذا فإن قسطا من الطاقة الميكانيكية الممنوحة للحبل يفقد، فيكتسبها الوسط الخارجي وذلك بمفعول الشغل المقاوم لقوى الإحتكاك، فيلاحظ خمود متوالي للموجة وينخفض وسع الموجة بالتدريج.
النص 28: خاصية الموجة المنعكسة
تتميز الموجة المستقيمية الواردة
بسرعة الانتشار c والتردد N وطول الموجة
λ، فهل للموجة المستقيمية المنعكسة نفس المميزات ؟
وللإجابة عن هذا التساؤل، نضيء سطح الماء لحوض الموجات بواسطة وماض يضبط على تردد
الومضات الذي يكمن من مشاهدة توقف ظاهري للموجة المستقيمية الواردة، نلاحظ أن:
-
الموجة المنعكسة تظهر أيضا متوقفة: إذن لها نفس التردد N
للموجة الواردة.
- الموجتين الواردة والمنعكسة تنتشران في نفس الوسط: إذن لهما
نفس سرعة الانتشار c.
- للموجتين الواردة والمنعكسة نفس
طول الموجة (لأن:
λ=c/N).
النص 29: ظاهرة الإنتقال في وسط ثلاثي البعد
بينت التجارب أن الموجات الصوتية المنتشرة في الهواء بسرعة الإنتشار c1 تخضع لظاهرة الإنتقال (الإنكسار) في السوائل بسرعة الانتشار c2. وتجدر الإشارة إلى أن السوائل تمتص أغلبية الموجات الواردة وتعكس جزءا منها، (تكون لدينا في هذه الحالة c1<c2 انظر رتب قدر سرعات انتشار الصوت في الموائع) إلا أن ظاهرة الإنتقال غير ممكنة في كل الحالات. حيث ظاهرة الانعكاس تصبح مهمة عندما تكون زاوية الورود أكبر من 13°، إذ يتصرف المستوى الكاسر كحاجز عاكس.
النص 30: خاصية الموجة المحيدة
للموجة
الواردة تردد N وسرعة انتشار c وطول
الموجة λ، فما هي مميزات الموجة المحيدة ؟
إن التوقف الظاهري
للموجتين الواردة والمحيدة تحت ضوء الوماض يدل على أن لهما نفس التردد N. وبما أنهما تنتشران في نفس وسط الإنتشار، فإن لهما نفس سرعة
الانتشار c ، ومنه نستنتج أن للموجتين نفس طول الموجة λ.
ويكمن أن نتحقق تجريبيا من ذلك بقياس المسافة بين خطي ذروتين
متتاليتين.
النص 31: انتشار الضوء
بينت عدة تجارب أن الضوء ينتشر في أوساط شفافة ومتجانسة وفق خطوط مستقيمية بين المنبع الضوئي والمستقبل، وهذا ما يسمى بمبدأ الإنتشار المستقيمي للضوء. ونشير إلى أن المنابع الضوئية ترسل حزما ضوئية مكونة من عدد غير محدود من الأشعة الضوئية، حيث يستحيل عزل شعاع ضوئي تجريبيا، بينما يصطلح على تمثيله بخط مستقيم يحمل سهما يدل على منحى انتشار الضوء.
النص 32: قانونا ديكارت للانعكاس
القانون الأول: يوجد الشعاع الوارد والشعاع المنعكس
والمنظمي على المرآة في مستوى واحد يسمى مستوى الورود.
القانون الثاني: عند
انعكاس الضوء، تساوي زاوية الانعكاس زاوية الورود.
* يطبق
قانونا ديكارت بالنسبة لسطح عاكس كيف ما كان شكله. وفي هذه الحالة يكون المنظمي هو
المنظمي على المستوى المماس للسطح العاكس في نقطة الورود.
النص 33: ظاهرة الإنكسار
نرسل على سطح ماء ملون، الذي يحتويه
حوض عميق من زجاج، حزمة ضوئية دقيقة تكون مع المنظمي على سطح الماء زاوية ورود غير
منعدمة، فيحدث تغيرا في اتجاه الحزمة الضوئية الواردة عند الحد الفاصل بين الهواء
والماء الملون، فنشاهد في آن واحد:
- حزمة ضوئية تنتشر في الهواء في اتجاه مخالف
لاتجاه الحزمة الواردة، وتسمى الحزمة الضوئية المنعكسة.
- حزمة ضوئية تنتشر في
الماء الملون في اتجاه مخالف لاتجاه الحزمة الواردة: إنها الحزمة الضوئية المنكسرة.
وتسمى هذه الظاهرة انكسار الضوء، التي تحدث كلما مر هذا الأخير عبر الحد الفاصل بين
الوسطين والذي نسميه سطحا كاسرا.
النص 34:
يتم حيود الضوء المنبعث من المنبع
S بواسطة الشقين S1 و S2 الذين يتصرفان كمنبعين ضوئيين مترابطين. وتتراكب
الحزمتان الضوئيتان المنبعثتان من S1 و S2 فتحدث ظاهرة التداخلات الضوئية. وقياسا على التداخلات
الميكانيكية على سطح الماء، فإن ظهور الأهداب المظلمة لا يمكن شرحها إلا باعتبار
الطبيعة الموجية للضوء. ويمكن أن عن ذلك بكيفية مبسطة كما يلي:
ضوء + ضوء =
ظلام.
وأن الأهداب المظلمة ناتجة عن تراكب الموجتين الضوئيتين المنبعثتين من
S1 و S2
، واللتين توجدان على تعاكس في الطور عند وصولهما إلى النقط التي تكون هذه
الأهداب: نقول إن التداخلات مهدمة.
أما الأهداب المضيئة
فناتجة عن تراكب الموجتين المنبعثتين من S1 و
S2 ، واللتين توجدان على توافق في الطور عند
وصولهما إلى النقط التي تكون هذه الأهداب: نقول إن التداخلات إنشائية.
![]()
النص :
يوجد نوعان رئيسيان من التفاعلات الكيميائية التي تحدث في المحاليل المائية:
- التفاعلات الحمضية - القاعدية التي تنتج عن تبادل البروتونات H+ بين الحمض والقاعدة المتواجدين في مذيب مائي.
- تفاعلات الأكسدة والإختزال في المحاليل المائية التي تنتج عن تبادل الإلكترونات. ونجد هذا النوع من التفاعلات بكثرة سواء في الكيمياء العضوية أو غير العضوية.
النص: تعريف الأكسدة والإختزال
نسمي أكسدة نوع كيميائي (ذرة أو جزيئة أو أيون) فقدان الإلكترونات من طرف هذا النوع خلال تفاعل كيميائي.
ونسمي اختزال نوع كيميائي اكتساب الإلكترونات من طرف هذا النوع خلال التفاعل.
يقوم النوع الكيميائي بدور المختزل حينما يفقد إلكترونات خلال التفاعل الكيميائي، بينما يقوم النوع الكيميائي بدور المؤكسد حينما يكتسب إلكترونات خلال التفاعل الكيميائي.
النص: عمود دانييل
عمود دانييل مولد كهربائي مستقطب ذو قوة كهرمحركة تساوي تقريبا 1,10v . يتكون العمود من قنطرة إلكتروليتية ونصفي عمود، يتألف كل منهما من مختزل الفلز، ومؤكسده المرافق، الكاتيون المميه.
النص: التموضع النسبي للمزدوجات
ليكن محور مدرج بالفولط وموجه في نفس منحى "محور تزايد القدرة المؤكسدة". نعلم أن القوة الكهرمحركة لعمود تمثل كذلك التوتر الفراغي. وهكذا
نكتب: ECu/Zn=VCu-VZn=1,10V وهذا يعني أن جهد إلكترود النحاس أعلى بـ 1,10V من جهد إلكترود
الزنك. ولاحترام فرق الجهد هذا يجب وضع، على المحور المدرج بالفولط، النقطة التي تمثل المزدوجة Cu2+/Cu فوق النقطة التي تمثل المزدوجة
Zn2+/Zn.
وبنفس الطريقة نحدد على المحور مواضع النقط التي تمثل باقي المزدوجات المدروسة. وهكذا نحدد بصفة كمية الترتيب الكهركيميائي للمزدوجات مؤكسد - مختزل.
النص: معايرة الأكسدة والاختزال
إن الغاية من معايرة الأكسدة والإختزال هي تعيين التركيز المولي الحجمي للمؤكسد أو المختزل في المحلول. وتتلخص هذه العملية
في تأثير محلول يحتوي على المؤكسد (أو المختزل) المراد معايرته على محلول ذي تركيز اختزالي (أو تأكسدي) معروف. مع العلم أن هذه المعايرة تكون ممكنة إذا كان تفاعل الأكسدة
والإختزال بين المحلولين تلقائيا وسريعا وكليا.
ويكون تفاعل الأكسدة والإختزال كليا كلما كان الفرق بين الجهدين المعياريين Δπ° للمزدوجتين المتواجدتين كبيرا،
وعمليا إذا كان Δπ° > 0,4 V
يسهل الحصول على تفاعل كلي وأحيانا سريع. ويمتاز أيون البرمنغنات بقدرة أكسدته لعدد كبير من الأنواع الكيميائية، وذلك لأن قيمة جهده المعياري مرتفعة.
النص: عدد التأكسد
القاعدة 1: عدد تأكسد العنصر في أيون بسيط يساوي عدد الشحنات الموجودة على الأيون مسبوقا بالإشارة التي تدل على نوع الشحنة.
القاعدة 2: عدد تأكسد العنصر في الأجسام البسيطة الأحادية الذرة أو المتعددة الذرات يساوي صفرا.
القاعدة 3: في جميع الأجسام المركبة، يساوي عدد تأكسد الهيدروجين (I+)، ويساوي عدد تأكسد الأوكسيجين (II-).
القاعدة 4:
- عندما تكون ذرتان مرتبطتان برابطة تساهمية، تسند اعتباطا الإلكترونات إلى الذرة الأكثر كهرسالبة. ويساوي إذا عدد تأكسد عنصر في مركب تساهمي الشحنة الإعتبارية التي أسندت
إليه.
- حسب انحفاظ الشحنة، يساوي المجموع الجبري لأعداد التأكسد، لجميع الذرات المكونة لجزيئة، صفرا.
القاعدة 5: المجموع الجبري لأعداد التأكسد لجميع الذرات المكونة لأيون متعدد الذرات، يكون مساويا للشحنة التي يحملها هذا الأيون.
النص: تركيب المواد العضوية
إن عدد المركبات العضوية هائل جدا بالقياس إلى عدد المركبات اللاعضوية. ورغم تنوع المركبات العضوية، فإنها لا تحتوي إلا على عدد محدود من العناصر:
- الكربون: يوجد في جميع المركبات العضوية.
- الهيدروجين: يصاحب الكربون في أغلب المركبات العضوية، حيث نجد عدة مركبات عضوية تتكون من الكربون والهيدروجين فقط. أمثلة: الميثان CH4 ،
البوتان C4H10 ، البنزين C6H6 .
- الأوكسجين: يوجد في بعض المركبات العضوية، أمثلة: الإيثانول C2H5OH ، حمض الإيثانويك C2H5COOH،
الدهون المكونة للزيوت والشحوم، والسكريات المشتملة عل السكر والنشا والسيليلوز ... تتكون من ثلاثة عناصر: C.H.O.
- الأزوت: وهو أقل وجودا من الأوكسيجين في المركبات العضوية.
- عناصر أخرى نادرة الوجود في المركبات العضوية: الهالوجينات والكبريت والفوسفور وبعض الفلزات
Mg, Fe, K, ...
النص: بعض الخصائص الكيميائية والفيزيائية للمركبات العضوية
إن وجود الرابطة التساهمية في أغلب المركبات العضوية يجعل خصائصها الفيزيائية والكيميائية تختلف عن خصائص المركبات اللاعضوية:
- المركبات العضوية أكثر تطايرا من المركبات اللاعضوية، أغلبها يوجد في الظروف العادية لدرجة الحرارة والضغط في الحالة الغازية كالغاز الطبيعي أو في الحالة السائلة كالكحول.
درجة حرارة انصهارها وغليانها منخفضة، وهي لا تتحمل درجة حرارة تفوق 500°C.
- لا تذوب المركبات العضوية على العموم في الماء ولكنها تذوب في المذيبات العضوية كالبنزين والكحول والإثير، وتستغل هذه الظاهرة في تنظيف الملابس والقطع المعدنية.
- المركبات العضوية غير موصلة للتيار الكهربائي، عكس المركبات اللاعضوية التي تنقله عندما تكون مذابة في الماء أو في حالة انصهار.
- تفاعلات المركبات العضوية عموما بطيئة وعكوسة بينما تفاعلات المركبات غير العضوية غالبا ما تكون سريعا وتامة.
النص: بنية جزيئة الميثان
الميثان مركب هيدروكربوني، وهو أول وأبسط مركب في مجموعة الألكانات. تتكون جزيئته من ذرة كربون واحدة وأربع ذرات هيدروجين. صيغته الإجمالية هي
CH4.
إن العدد الذري لذرة الكربون هو Z=6، وحسب التوزيع الإلكتروني لذرة الكربون فإن مستوى الطاقة الخارجي (L)
لهذه الذرة يحتوي على أربع إلكترونات. أما العدد الذري لذرة الهيدروجين فهو Z=1، وحسب التوزيع الإلكتروني لهذه الذرة فإن مستوى الطاقة الخارجي
(K) يحتوي على إلكترون واحد.
ولتحصل ذرة الكربون على البنية الإلكترونية للغاز الخامل الأقرب في الترتيب الدوري (النيون)، القاعدة الثمانية، تشرك إلكتروناتها الأربعة الخارجية مع أربع
إلكترونات لأربع ذرات هيدروجين مكونة بذلك جزيئة
الميثان. فيشبع بذلك مستوى الطاقة الأول (K) لكل ذرة هيدروجين بإلكترونين، ويشبع المستوى (L) لذرة الكربون بثمانية إلكترونات.
وهكذا تكون لذرة الكربون وذرات الهيدروجين نفس القابلية في إشراك إلكترونات لتكوين روابط تساهمية بسيطة ممثلة حسب نموذج لويس (LEWIS) بأربعة أزواج
إلكترونية حيث يكون كل زوج رابطة تساهمية بسيطة نمثلها بخط صغير (-) بين ذرة الكربون وذرة الهيدروجين.
إن ذرة الكربون رباعية التكافؤ لأن لها قابلية تأليف أربعة روابط تساهمية.
النص: الخواص الفيزيائية للألكانات
تتغير الخواص الفيزيائية للألكانات العادية بانتظام، فعند درجة الحرارة 20°C وتحت الضغط الجوي العادي تكون المركبات الأربعة الأولى (الميثان والإيثان والبروبان والبوتان) في حالة غازية ثم سوائل من البنتان C5H12 إلى البنتاديكان C15H32 وصلبة عندما يفوق عدد ذرات الكربون في الألكان 15. وتجدر الإشارة إلى أن الألكانات ذات السلسلة المتفرعة لها درجة حرارة الغليان أصغر من درجة حرارة غليان متماكباتها ذات السلسلة الخطية. إن أغلب الألكانات قليلة الذوبان في الماء (فمثلا لتر واحد من الماء لا يذيب سوى 40cm3 من الميثان) والألكانات السائلة أخف من الماء مما يجعلها تطفو على سطح الماء.
النص: هلجنة الألكانات
ينتمي تفاعل الإستبدال بالكلور أو الكلورة إلى تفاعلات الهلجنة أي تفاعلات استبدال ذرات الهيدروجين بذرات الهالوجينات. ونذكر أن الهالوجينات تضم عناصر الفلور F والكلور Cl والبروم Br واليود I. وبصفة عامة أثناء كل تفاعل استبدال لا تتحطم الرابطة C-C، بينما يمكن لبعض الروابط C-H أن تتكسر لتعطي روابط جديدة C-X حيث X ذرة هالوجين.
النص: تعريف الألكينات
الألكينات هي هيدروكربورات غير مشبعة ذات سلسلة كربونية مفتوحة، تحتوي جزئياتها على رابطة تساهمية ثنائية. وبصفة عامة تنقص مجموعة الألكينات بالنسبة إلى مجموعة الالكانات ذرتان من الهيدروجين، فتكون صيغتها الإجمالية العامة هي CnH2n حيث n عدد صحيح يساوي أو يفوق 2.
النص: تعريف الألسينات
الألسينات هي هيدروكربورات غير مشبعة ذات سلسلة كربونية مفتوحة، تحتوي جزئياتها على رابطة ثلاثية واحدة، إذ تنقصها بالنسبة إلى مركبات الألكينات التي تقابلها ذرتان من الهيدروجين، صيغتها الإجمالية العامة هي CnH2n-2 حيث n عدد صحيح يساوي أو يفوق 2.
النص:
نسمي تفاعل الإضافة التفاعل الذي يتم فيه تثبيت جزيئة على جزيئة أخرى. وتتحول فيه الرابطة المضاعفة (الثنائية أو الثلاثية) بين ذرتي الكربون إلى رابطة
بسيطة.
تفاعل البلمرة من بين تفاعلات الإضافة المهمة التي تعطيها المركبات الهيدروكربونية غير المشبعة هناك تفاعل خاص تتحد فيه عدة جزيئات من نفس النوع فيما بينها لتعطي جزيئة
ذات سلسلة كربونية طويلة. نسمي هذا التفاعل بلمرة ونعبر عنه بالمعادلة:
nM→Mn
النص: التفاعلية الخاصة للمركبات الأروماتية
تعطي المركبات الأروماتية:
. تفاعلات احتراق مثل جميع المركبات العضوية.
. تفاعلات إضافة مثل الهيدروكربورات ذات السلسلة الكربونية غير المشبعة.
. تفاعلات الإستبدال مثل الهيدروكربورات ذات السلسلة المشبعة.
النص: الكحولات
الكحولات اسم عربي أطلق لأول مرة على الكحول الإثيلي (الإيثانول) الذي كان يحصل عليه بتخمر العنب. والكحول الإثيلي سائل متطاير عديم اللون، له رائحة متميزة وهو أخف من الماء. ينحل في الماء مع نقصان في حجم المحلول وارتفاع في حرارته. والكحولات مذيبات جيدة لكنها مواد سامة وأخطرها الميثانول الذي يتسبب تناوله في فقدان البصر وكذلك الموت.
النص: الألدهيدات والسيتونات
تعتبر السيتونات متماكبات للألدهيدات حيث إن الصيغة العامة للألدهيدات والسيتونات المشبعة هي: CnH2nO .
النص: مفهوم التوازن الكيميائي
إن الأسترة والحلمأة تفاعلان لهما مميزات متقاربة جدا ويحدثان في نفس الظروف. فنواتج التفاعل الأول تلعب دور المتفاعلات في التفاعل الثاني، ونقول إن هذين التفاعلين متعاكسان ومحدودان، فتفاعل الأسترة يكون محدودا بسبب تفاعل حلمأة الإستير والعكس كذلك. ونقول أيضا إن الأسترة والحلمأة تفاعلان عكوسان. عندما تصل الأسترة (أو الحلمأة) إلى حدها يكون الخليط المتفاعل متكونا دائما، في كلتا الحالتين، من الحمض والكحول والإستير والماء، ولا يتغير تركيبه مع الزمن: نقول إنه حدث توازن كيميائي.
العناصر الكيميائية (الرموز والكتل الذرية)
اسم العنصر |
الرمز |
الكتلة |
اسم العنصر |
الرمز |
الكتلة |
||
| Actinium | أكتينيوم | Ac | 227 | Molybdène | موليبدن | Mo | 95,9 |
| Aluminium | ألومينيوم | Al | 27,0 | Néodyme | نيوديم | Nd | 144,2 |
| Antimoine | أنتموان | Sb | 121,8 | Néon | نيوم | Ne | 20,2 |
| Argent | فضة | Ag | 107,9 | Nikel | نيكل | Ni | 58,7 |
| Argon | أرغون | A | 39,9 | Niobium | نيوبيوم | Nb | 92,9 |
| Arsenic | زرنيخ | As | 74,9 | Or | ذهب | Au | 197,0 |
| Astate | أستات | At | 210 | Osmium | أوسميوم | Os | 190,2 |
| Azote | أزوت | N | 14,0 | Oxygène | أوكسيجين | O | 16,0 |
| Baryum | باريوم | Ba | 137,3 | Paladium | بلاديوم | Pd | 106,4 |
| Bérylium | بيريليوم | Be | 9,0 | Phosphore | فوسفور | P | 31,0 |
| Bismuth | بزموت | Bi | 209 | Platine | بلاتين | Pt | 195,1 |
| Bore | بور | B | 10,8 | Plomb | رصاص | Pb | 207,2 |
| Brome | بروم | Br | 79,9 | Polonium | بولونيوم | Po | 210 |
| Cadmium | كادميوم | Cd | 112,4 | Potassium | بوتاسيوم | K | 39,1 |
| Calcium | كالسيوم | Ca | 40,1 | Praséodyme | براسيوديم | Pr | 140,9 |
| Carbone | كربون | C | 12,0 | Prométhium | بروميثيوم | Pm | 145 |
| Cérium | سيريوم | Ce | 140,1 | Protactinium | بروتاكتينيوم | Pa | 231 |
| Césium | سيزيوم | Cs | 132,9 | Radium | راديوم | Ra | 226 |
| Chlore | كلور | Cl | 35,5 | Radon | رادون | Rn | 222 |
| Chrome | كروم | Cr | 52,0 | Rhénium | رينيوم | Re | 186,2 |
| Cobalt | كوبالت | Co | 58,9 | Rhodium | روديوم | Rh | 102,9 |
| Cuivre | نحاس | Cu | 63,5 | Rubidium | روبيديوم | Rb | 85,5 |
| Dysprosium | ديسبروسيوم | Dy | 162,5 | Ruthénium | روثينيوم | Ru | 101,1 |
| Erbium | إيربيوم | Er | 167,3 | Smarium | سماريوم | Sm | 150,4 |
| Etain | قصدير | Sn | 118,7 | Scandium | سكانديوم | Sc | 45,0 |
| Europium | أوروبيوم | Eu | 152 | Sélénium | سيلينيوم | Se | 79,0 |
| Fer | حديد | Fe | 55,8 | Silicium | سيليسيوم | Si | 28,1 |
| Fluor | فلور | F | 19,0 | Sodium | صوديوم | Na | 23,0 |
| Francium | فرانسيوم | Fr | 223 | Soufre | كبريت | S | 32,1 |
| Gadolinium | غادولينيوم | Gd | 157,3 | Strontium | سترونتيوم | Sr | 87,6 |
| Gallium | غاليوم | Ga | 69,7 | Tantale | تنتال | Ta | 180,9 |
| Germanium | جرمانيوم | Ge | 72,6 | Téchnétium | تكنيسيوم | Tc | 99 |
| Hafnium | هافنيوم | Hf | 178,5 | Tellure | تلور | Te | 127,6 |
| Hélium | هيليوم | He | 4,0 | Terbium | تيربيوم | Tb | 158,9 |
| Holmium | هولميوم | Ho | 164,9 | Tallium | تاليوم | Tl | 204,4 |
| Hydrogène | هيدروجين | H | 1,0 | Thorium | توريوم | Th | 232,0 |
| Indium | أنديوم | In | 114,8 | Thulium | توليوم | Tm | 168,9 |
| Iode | يود | I | 126,9 | Titane | تيتان | Ti | 47,9 |
| Iridium | إيريديوم | Ir | 192,2 | Tungstène | تنغستين | W | 183,9 |
| Krypton | كريبتون | Kr | 83,8 | Uranium | أورانيوم | U | 238,0 |
| Lanthane | لانتان | La | 138,9 | Vanadium | فاناديوم | V | 50,9 |
| Lithium | ليثيوم | Li | 6,9 | Xénon | كزينوم | Xe | 131,3 |
| Lutécium | لوتيسيوم | Lu | 175,0 | Ytterbium | إيتيربيوم | Yb | 173 |
| Magnésium | مغنيزيوم | Mg | 24,3 | Yttrium | إيتريوم | Y | 88,9 |
| Manganèse | منغنيز | Mn | 54,9 | Zinc | زنك | Zn | 65,4 |
| Mercure | زئبق | Hg | 200,6 | Zirconium | زيركونيوم | Zr | 91,2 |
![]()
1- الهندسة
النص:
لتكن (C)
دائرة شعاعها 3cm. في كل من الحالتين:
α=π/9rad؛ α=18°.
- احسب طول القوس الهندسية ثم مساحة القطاع الدائري المحصور بالزاوية التي قياسها
α.
لتكن (C) شعاعها 1m.
في كل الحالتين: α=π/8rad ؛ α=36° .
- احسب طول القوس الهندسية التي تحصر الزاوية المركزية التي قياسها
α.
. ما هو القياس بالراديان وبالدرجة لزاوية مركزية طول قوسها
3,5cm ؟
- ما هي مساحة الجزء المخدش ؟
- احسب بالراديان والدرجة قياسات زوايا مخمس منتظم.
النص: الأفصول المنحني
- لتكن M نقطة من دائرة مثلثية (C) أصلها I. وليكن a طول القوس الذي طرفاه I و M بالذهاب من I إلى M في المنحى الموجب. كل عدد يكتب على الشكل a+k.2π أو (a+2kπ) بحيث k عنصر من Z يسمى أفصولا منحنيا للنقطة M.
النص: دالة جيب التمام ودالة الجيب ودالة الظل
- الدالة العددية التي
تربط بكل عدد حيقي x جيب تمامه تسمى دالة جيب التمام. ويرمز
لها بالرمز cos.
وهكذا فإن: cos:
x→cosx.
- الدالة العددية التي تربط بكل عدد حقيقي x جيبه تسمى دالة
الجيب. ويرمز لها بالرمز sin .
وهكذا فإن : sin: x→sinx.
- الدالة العددية التي تربط بكل عدد حقيقي x يخالف
π/2+kπ حيث k عنصر من
Z ، ظله تسمى دالة الظل. ويرمز لها بالرمز
tan.
وهكذا فإن : tan: x→tanx.
النص:
معادلة مستقيم معرف بنقطة
وبمتجهة منظمية عليه
- لتكن 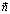 متجهة غير منعدمة و
A نقطة من المستوى. مجموعة النقط M
من المستوى التي تحقق العلاقة
متجهة غير منعدمة و
A نقطة من المستوى. مجموعة النقط M
من المستوى التي تحقق العلاقة 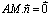 هي المستقيم
المار من النقطة A و
هي المستقيم
المار من النقطة A و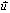 متجهة موجهة له.
متجهة موجهة له.
- المستوى منسوب لمعلم متعامد ممنظم
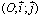 . إذا
كان (D) مستقيما مارا من النقطة A و
. إذا
كان (D) مستقيما مارا من النقطة A و
 متجهة منظمية عليه فإن:
متجهة منظمية عليه فإن:
a(x-x0)+b(y-y0)=0 معادلة
ديكارتية له.إذا كان (D) مستقيما ax+by+c=0
معادلة ديكارتية له فإن المتجهة
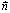 متجهة منظمية عليه.
متجهة منظمية عليه.
النص: تمرين
المستوى منسوب لمعلم متعامد ممنظم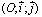 .
.
D مستقيم من المستوى بحيث 3x-5y+2=0 معادلة
ديكارتية له. و P نقطة من المستوى P
.
- أنشئ المستقيم D.
- حدد معادلة ديكارتية للمستقيم Δ
المار من النقطة P وعمودي على المستقيم D
ثم حدد زوج إحداثيتي النقطة H تقاطع المستقيمين
D و Δ . ماذا تمثل النقطة H بالنسبة
للنقطة P.
- احسب المسافة HP، مسافة النقطة P
عن المستقيم D.
النص: تقاطع دائرة ومستقيم:
1.
D مستقيم في المستوى وC دائرة في
المستوى مركزها Ω وشعاعها r. تقاطع المستقيم
D والدائرة C هو:
- المجموعة الفارغة إذا كان d(Ω,D)>r .
- أحادية إذا كان d(Ω,D)=r.
- مجموعة من نقطتين إذا كان d(Ω,D)<0.
2. نقول إن المستقيم D للدائرة C عند النقطة A إذا كان عموديا على المستقيم ΩA في النقطة A.
3. المستوى P منسوب لمعلم متعامد ممنظم. إذا كانت C دائرة في المستوى معادلتها: x2+y2-2ax-2by+c=0 فإن معادلة المماس لها عند النقطة A هي: xx0+yy0-a(x-x0)-b(y+y0)+c=0.
النص: تمرين
تحديد معادلة
مماسين لدائرة والمارين من نقطة خارجها.
في المستوى المنسوب لمعلم متعامد ممنظم، نعتبر الدائرة C
التي معادلتها x2+y2-4x-2y=0 و
A(3,-2) نقطة من المستوى.
أ- تحقق من أن النقطة A توجد خارج الدائرة
C.
ب- أوجد معادلتي المماسين للدائرة C المارين من النقطة
A وحدد زوجي إحداثيتي نقطتي التماس.
النص: الدوران الذي زاويته منعدمة
ليكن
r دورانا مركزه O وزاويته α.
إذا كان α≡0[2π] فإن صورة كل نقطة
M هي نفسها.
وفي هذه الحالة يكون الدوران r هو التطبيق المطابق في
المستوى أي: جميع نقط المستوى تكون صامدة بهذا التطبيق.
أما إذا كان α≠0[2π] فإن النقطة الصامدة الوحيدة
بالدوران r هي المركز O.
النص: تمرين
ليكن
ABC مثلثا و 'A'B'C صورته بدوران
r.
ليكن ['AA] و [AI] و
[AD] على التوالي الإرتفاع والمتوسط والمنصف المارين من
الرأس A و (Δ) واسط الضلع [BC].
بين أن صورة القطع ['AA] و [AI]
و [AD] هي على التوالي الإرتفاع والمتوسط والمنصف
للمثلث 'A'B'C المارين من 'A وأن
صورة (Δ) هي واسط الضلع ['B'C].
النص: الإسقاط على مستقيم بتواز مع مستوى
نعتبر مستقيما D ومستوى P غير متوازيين. لتكن M نقطة من الفضاء ε . أنشئ المستوى Q المار من M والموازي للمستوى P. Q يقطع D في نقطة 'M لأن Q يوازي P و P يقطع D. من كل نقطة M في الفضاء يمر مستوى Q يوازي P ويقطع D في نقطة وحيدة 'M. نسمي 'M مسقط M على المستقيم D بتواز مع المستوى P ، وبما أنه يمكن ربط كل نقطة M في الفضاء ε بمسقطها 'M على D بتواز مع P فإننا نكون قد عرفنا تطبيقا من ε نحو ε يسمى الإسقاط على المستقيم D بتواز مع المستوى P.
النص: المعادلة المتجهية لمستقيم
A نقطة من الفضاء و
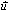 متجهة غير منعدمة،
D(A,
متجهة غير منعدمة،
D(A,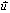 )
هي مجموعة النقط M من الفضاء بحيث تكون المتجهتان
)
هي مجموعة النقط M من الفضاء بحيث تكون المتجهتان
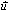 و
AM مستقيمية.
و
AM مستقيمية.
- إذا كانت 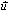 متجهة
موجهة للمستقيم D فإن كل متجهة مستقيمية مع
متجهة
موجهة للمستقيم D فإن كل متجهة مستقيمية مع
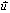 هي أيضا متجهة موجهة له.
هي أيضا متجهة موجهة له.
- إذا كانت C و D نقطثين مختلفتين
من المستقيم D فإن
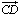 متجهة موجهة له.
متجهة موجهة له.
2- التحليل
النص:
- عندما نقول
f دالة عددية معرفة على D فإن ذلك
يعني أن مجموعة تعريف الدالة f تحتوي على المجموعة
D.
- الدالة التآلفية هي كل دالة معرفة على IR بما يلي:
F(x)=ax+b. حيث a و
b عددان حقيقيان.
- منحى دالة تآلفية في المستوى المنسوب إلى معلم هو مستقيم.
النص: تعريف الدالة الزوجية والدالة الفردية
الدالة الزوجية:
- لتكن f دالة عددية و C منحناها
في معلم متعامد . تكون الدالة f زوجية إذا وفقط إذا كان
C متماثلا بالنسبة لمحور الأراتيب.
الدالة الفردية:
- لتكن f دالة عددية و C منحناها في
معلم ما. تكون f فردية إذا وفقط إذا كان C
متماثلا بالنسبة لأصل المعلم.
النص: معدل تغير دالة
لتكن f دالة
عددية معرفة على مجموعة I. ليكن x1
و x2 عنصرين مختلفين من I
.
العدد الحقيقي T=[f(x2)-f(x1)]/(x2-x1)
يسمى معدل تغير f بين x1
و x2 .
- f تزايدية على I إذا وفقط إذا كان
T≥0
لكل عنصرين مختلفين من I.
- f تزايدية قطعا على I إذا وفقط
إذا كان T>0 لكل عنصرين مختلفين من I.
- f تناقصية على I إذا وفقط إذا كان
T≤0 لكل عنصرين مختلفين من I.
- f تناقصية قطعا على I إذا وفقط
إذا كان T<0 لكل عنصرين مختلفين من I.
النص: التأويل المبياني
لتكن f دالة معرفة على D.
تكون f موجبة على D إذا وفقط إذا
كان المنحنى الممثل لها على D في معلم ما يوجد في نصف
المستوى الذي أراتيب نقطه موجبة.
ونقول تجاوزا أن منحى f يوجد فوق محور الأفاصيل.
تكون f سالبة على D إذا وفقط إذا
كان المنحنى الممثل لها على D في معلم ما يوجد في نصف
المستوى الذي أراتيب نقطه سالبة.
ونقول تجاوزا إن منحى f يوجد تحت محور الأفاصيل.
النص: دالة مكبورة - دالة مصغورة - دالة محدودة
لتكن f دالة عددية معرفة على مجموعة D.
نقول إن f مكبورة على D إذا وجد عدد
حقيقي M بحيث f(x)≤M لكل
x من D.
نقول إن f مصغورة على D إذا وجد عدد
حقيقي m بحيث f(x)≥m لكل
x من D.
نقول إن f محدودة على D إذا وجد
عددان حقيقيان m و M بحيث
m≤f(x)≤M لكل x من
D.
النص: تمرين
لكل عدد حقيقي
m نعتبر الدالة fm
المعرفة على IR بما يلي: fm(x)=mx+1
والدالة gm المعرفة على IR
بما يلي: gm(x)=x+m.
1. ارسم التمثيل المبياني للدوال f1 و
f2 و f3 ماذا
تلاحظ ؟
2. بين أن التمثيلات المبيانية للدوال fm تمر
بنقطة ثابتة.
3. حدد بدلالة m احداثيتي نقطة تقاطع التمثيل المبياني
للدالة fm والتمثيل المبياني للدالة
gm مع
(m≠1).
النص: النصوص الرياضية
يمكن تقسيم النصوص
الرياضية التي تعتبر صحيحة على الشكل التالي:
. المسلمات (أو الفرضيات): وهي نصوص رياضية تعتبر صحيحة بدون برهان وتكون أساسا
للنظرية الرياضية المعتمدة باعتبار أن لكل نظرية مسلماتها الخاصة بها.
. التعاريف: وهي نصوص رياضية تعرف بعض العناصر الرياضية والخاصيات التي تتوفر
عليها.
. المبرهنات والخاصيات: وهي نصوص رياضية يتم البرهان على صحتها عن طريق الإستدلال
الرياضي (أو المنطق) بالإعتماد على المسلمات والتعاريف ونتائج أخرى سبق البرهان على
صحتها.
النص: المكممات والعبارات المكممة
لتكن A(x) دالة عبارية للمتغير
x و E مجموعة غير فارغة.
- انطلاقا من A(x) ننشأ العبارة
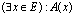 التي تكون صحيحة فقط إذا كان
يوجد على الأقل عنصر واحد من E يحقق الخاصية
A(x).
التي تكون صحيحة فقط إذا كان
يوجد على الأقل عنصر واحد من E يحقق الخاصية
A(x).
. الرمز З يسمى المكمم الوجودي.
. العبارة 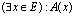 تقرأ "يوجد على الأقل عنصر
x من E يحقق
A(x)".
تقرأ "يوجد على الأقل عنصر
x من E يحقق
A(x)".
- وانطلاقا من A(x) ننشأ أيضا العبارة 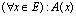 التي تكون صحيحة فقط إذا كان جميع عناصر المجموعة E تحقق
الخاصية A(x).
التي تكون صحيحة فقط إذا كان جميع عناصر المجموعة E تحقق
الخاصية A(x).
. الرمز Y يسمى المكمم الكوني.
. العبارة 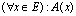 تقرأ:
مهما يكن العنصر x من E لدينا:
A(x). أو : لكل عنصر x من
E لدينا : A(x).
تقرأ:
مهما يكن العنصر x من E لدينا:
A(x). أو : لكل عنصر x من
E لدينا : A(x).
النص:
- تكون دالة
f متصلة على اليمين في x0
إذا وفقط إذا كانت لها نهاية على اليمين في x0
تساوي f(x0).
- تكون دالة f متصلة على اليسار في x0
إذا وفقط إذا كانت لها نهاية على اليسار في x0
تساوي f(x0).
- تكون دالة f متصلة في x0
إذا وفقط إذا كانت متصلة على اليسار وعلى اليمين في x0.
النص:
1- نقول إن
دالة f قابلة للاشتقاق على مجال مفتوح I
إذا كانت قابلة للاشتقاق في كل نقطة من المجال I.
2- نقول إن دالة f قابلة للاشتقاق على مجال مغلق
[a,b] إذا كانت قابلة للاشتقاق على المجال المفتوح
]a,b[ وقابلة للاشتقاق عل اليمين في a
وعلى اليسار في b.
3- لتكن f دالة قابلة للاشتقاق على مجال I
. الدالة المعرفة على I بما يلي: I→IR
و x→f(x). تسمى الدالة المشتقة
للدالة f على المجال I ويرمز لها ب:
'f.
4- نعتبر دالة f قابلة للاشتقاق على مجال I
. إذا كانت الدالة المشتقة 'f قابلة الاشتقاق على
I فإن دالتها المشتقة تسمى الدالة المشتقة الثانية للدالة
f على المجال I ويرمز لها ب:
''f.
النص:
f دالة قابلة للاشتقاق مرتين على مجال I
وC هو المنحنى الممثل للدالة f.
- إذا كانت ''f موجبة على المجال I
فإن C يكون محدبا على I.
- إذا كانت ''f سالبة على المجال I
فإن C يكون مقعرا على I.
- إذا كانت ''f تنعدم في نقطة x0
من I وتتغير إشارتها فإن النقطة
M0(x0,f(x0) نقطة انعطاف للمنحنى
C.
النص: تصميم دراسة دالة
1- تحديد
مجموعة تعريف الدالة f ثم تحديد المجموعة التي ستدرس فيها
الدالة f. (خاصة إذا كانت f فردية
أو زوجية أو دورية).
2- تحديد النهايات عند محدات مجموعة الدراسة.
3- دراسة الاتصال وقابلية الاشتقاق. دراسة منحى تغيرات الدالة f
باستعمال الدالة المشتقة إذا كان ذلك ضروريا.
4- وضع جدول تغيرات الدالة f. إذا أردنا أن نرسم المنحنى
الممثل للدالة f فغالبا ما ندرس ما يلي:
5- الفروع اللانهائية.
6- تقعر المنحنى والبحث عن نقط الإنعطاف (إذا كان ذلك ضروريا).
7- تحديد العدد اللازم من النقط التي تنتمي إلىالمنحنى.
8- رسم المنحنى.
النص: تمرين
نعتبر الدال f المعرفة بما يلي: f(x)=y.
وليكن C منحنى الدالة f في معلم
متعامد ممنظم.
1- ادرس الدالة f (النهايات - التغيرات).
2- ادرس الفروع اللانهائية للمنحنى C.
3- . ادرس الوضع النسبي للمنحنى C والمستقيم الذي معادلته
y=x عندما يكون x<-1.
. ادرس الوضع النسبي للمنحنى C والمستقيم الذي معادلته
y=1 عندما يكون x>-1.
4- ادرس تقعر المنحنى C في كل من المجالين
]-1,+∞[ و ]-∞,-1[.
5- حدد نقط تقاطع المنحنى C ومحور الأفاصيل.
6- انشأ المنحنى C.
![]()